Can You Predict Where The Ball Will Land In Roulette?

Many games of chance have been the object of academic study in what concerns strategic play, but none have captured the interest of scientists in so many disciplinary directions as roulette has. Associated with the birth of probability theory (the origin of the game being attributed to Blaise Pascal, the early father of this theory), roulette as a topic of investigation for academics extended beyond mathematics.

When both experts and gamblers studied the game enough to conclude that no mathematical theory or application is able to beat the house or at least provide an optimal strategy of playing it (unlike in other games, such as blackjack or poker) and the excitement around the progressive systems like the martingale faded or died with the dismantling of their effectiveness, people turned their interest to the only possibility remaining – that of finding objective methods for predicting the outcomes of roulette.

Roulette is the only casino game with a mere deterministic nature, in the sense that the mechanical setup of generating the outcomes is entirely visible, measurable, and analysable in an inferential/deductive way. This of course is true for classical croupier-, mechanically- or electromechanically-spun roulette and not for electronic roulette with RNG (random number generator). Under these conditions, it is fair to think that one is able to conceive theoretical models and theories within a physics framework for studying whether roulette’s determinism can really be exploited for profit.

In this article we will make a brief overview of the history of such scientific endeavours of predicting the outcomes of roulette and see to what extent they are accurate and applicable in the real word of gambling.

The statistical exploit

There are two possible methods of exploiting roulette in regard to prediction: One is statistical in nature and relies on the imperfection of the physical setup of the roulette – unbalanced wheel, incline table, non-uniform rotation, and so on.

In such conditions of imperfection, it is expected that the roulette outcomes will not be uniformly distributed over the long run, as they were in conditions of physical perfection; in other words, randomness is broken and as such some outcomes might be favoured. This hypothesis can be tested by statistical observation and recording, by which we can find the segments of the wheel that the ball land in more frequently than in others.

Such statistical method is not specific to roulette. It applies to other games of chance and in experimental physics as well. For instance, by statistical observation one may retrieve the parametric configuration of a slot machine (the number of stops and the weighting of the symbols on the reels) for which its PAR sheet is kept secret.

Of course, the result of such an analysis would not be used for any prediction in the case of slots, but just for finding the probabilities of occurrence of the winning combinations.

As a consequence of such statistical exploits, casino managers did the utmost to avoid them and it’s hard to believe that in present days one can use that method effectively, also given the advancement of the table technology of construction.

The other method is inherently deterministic and consists of theoretical modelling in a mechanics framework.

In the early modern and contemporary history of the casinos, it was common for the roulette mechanisms to be imperfect; some imperfections were actually intentionally created for the house to cheat on gamblers, while others were simply the image of a poor technology or care. But some people were about to change that.

Early successes by statistical method

In 1873, an English mechanic and amateur mathematician called Jagger hypothesized that a slight imperfection in a roulette wheel could lead to sufficient edge for a profitable play and he took action: He went to the Monte Carlo casino with six assistants and recorded the outcome of each spin of six roulette tables for five weeks.

Analysis of the data showed that for each wheel there was a systematic bias favouring certain sectors of the wheel. Exploiting these biases, he gambled profitably for a week before the casino staff shuffled the wheels between tables. The tale says that he came away with £65,000 as profit.

In 1947 two students, Albert Hibbs and Roy Walford, found and exploited statistically imperfections and irregularities at roulette tables in the casinos in Reno, Nevada, during their vacation. The casino managers eventually threw them out after finding what they were doing, but they left with enough money to pay their Medical School taxes and buy a yacht and a house, as the tale says.

Such successful attempts have been repeated in various locations over time (being reported in the press) and the phenomenon captured the attention of the statistician Karl Pearson even since the end of the 19^th century, who provided an extensive statistical analysis and built the theoretical framework for the analysis and interpretation of the biased-roulette data.

The deterministic exploit

This method assumes theoretical work by building a theoretical model of the roulette motion, which to be applicable in the real situations for predicting the outcome of roulette. This model consists of the physical description of the investigated dynamical system in terms of mechanics – motions, forces, geometry of the components – by using physical quantities such as mass, velocities, acceleration, and so on.

Then, application of the model assumes the input of initial conditions in the form of measured values (initial positions of the wheel and ball, initial velocity of the ball, and so on) and derivation of a prediction (more or less larger segment of the wheel or even a precise pocket) by means of computation.

Such an application is made possible because placing the bets in roulette is traditionally allowed until some time after the ball and wheel are in motion.

The deterministic method does not use the mathematics directly (as the statistical method does), but the physics of roulette. However, mathematics is still constitutive for the equations describing the dynamical system.

The deterministic method captured the interest of several mathematicians, physicists, and engineers. And it was not just about an intellectual game and pleasure of solving a theoretical problem, but they actually aimed for the method to be effectively applicable, that is, to predict the outcomes of roulette with maximal accuracy, for the players to get a significant edge over the house.

Yet applicability turned out to be the biggest challenge for the deterministic method, because the more accurate the theoretical descriptions of the system were, the more difficult was to get the model applied for actual predictions, since application requires as a prerequisite all kind of precise measurements of the physical quantities involved.

Landmarks for the deterministic method

It was the famous mathematician Henri Poincaré the first who setup the theoretical foundation of such endeavours in 1914. In his seminal work Science and Method, Poincaré explained the principle that a small change in initial conditions can lead to a large change in effect, in relation with the nature of chance, and illustrated with the example of roulette. The concept of sensitivity to initial conditions is now a foundational stone of modern chaos theory.

However, a general theoretical procedure for predicting the outcome of roulette was described by Edward Thorp, the creator of the high-low count blackjack optimal strategy, in 1969. Together with Claude Shannon (the father of information theory), Thorp found that if the roulette wheel is not perfectly level (a tilt of 0.2 degrees was apparently sufficient according to tests) then there is a large portion of the frame from which the ball will not fall onto the wheel. They observed that condition met in about one third of the roulette wheels in Las Vegas. They claimed that in such cases it is possible for the gamblers to get an expected return of +15%, which increased to +44% with the aid of a ‘pocket-sized’ computer.

In 1967, mathematician Richard Epstein claimed that by measuring the angular velocity of the ball relative to the wheel he was able to predict correctly the half of the wheel into which the ball would fall. An important achievement was that he showed that the initial velocity of the ball is not decisive and the problem reverts to predicting when the ball will leave the outer rim as this will always occur at a fixed velocity. It is hypothesized that Epstein’s experiments were not done in real time, due to the lack of computational resources, and not attempted within a casino.

Scientists getting rich with the deterministic method

A more publicized attempt was that of a group of physicists among which Doyne Farmer and Normal Packard, who in 1977-1978 implemented their model and system on a 6502 microprocessor hidden in a shoe and applied them at several casinos in Las Vegas.

In 2004 news exploded in the media about three gamblers arrested after winning £1,300,000 at the Ritz casino in London. They had been using a laser scanner and cell phones to predict the outcome of roulette, according to a certain deterministic model. They were eventually found not guilty as to have broken no laws and remained with the money.

All these attempts and similar other not presented here had been based on deterministic models for the dynamical system of roulette. Those reported in the news, but also in academic papers, were the most successful, however not all came to reach effectiveness. This is because – on the one hand – the theoretical models were different to each other – they had different degrees of complexity, even different variables, and thus different capacity to reflect adequately the real phenomenon.

On the other hand and as important as the theoretical setup, application of the models and the actual implementation for a prediction in a casino assumes first that the values of the physical quantities reflecting the initial conditions are measurable and second that the means by which such measurements are performed are applicable and enough accurate.

This is why the technology of measurement is essential, for both measurement and computation. In addition, too many variables – while contributing to the adequacy of the model – pose practical problems to application.

A reference model for predicting the outcome of roulette

In 2012, two researchers (Michael Small, mathematician, and Chi Kong Tse, engineer) showed that only a few physical variables are sufficient in describing the motion of a roulette wheel and ball such that to allow prediction of the outcome with enough accuracy to achieve a positive expected return. These variables are: initial position, velocity, and acceleration.

The physical model they proposed for demonstrating their claim is conceived on the basis of various approximations and idealizations, which makes it less complex that other models and – what is important – applicable for actual prediction. They conceived two models, one for a level table and other for a crooked table. The models are not 100% deterministic, as some of the idealizations are of statistical nature – and this is one of the elements of originality of their work.

To argue for applicability, the authors made their own experiments, showing that even a manual implementation of is possible for their models. They showed that by applying the proposed techniques, at least 18% return is possible for the European roulette (instead of the theoretical –2.7% expectation). They published their results in the Chaos journal.

The model for the level table describes the system in three stages of motion: 1. Ball rotates in the rim. 2. Ball leaves the rim. 3. Ball rotates freely on the stator. 4. Ball reaches the deflectors.

There are some theoretical and procedural aspects and observations that make this model workable, among which the main important are:

• Time is considered as the core variable and not position.
• The angular position of the ball rotating in the rim decays only due to rolling friction.
• Each spin of the ball alters only the time spent in the rim and the ball will leave the rim with exact the same velocity each time. The descent of the ball from this point to the deflectors will thus be identical.
• The exact position of the wheel when the ball reaches a deflector is random, but will depend only on the angular position of the wheel at the time of hitting the deflector.

These aspects together with the necessary idealizations yield the equations of motion for this dynamical system, in which the metrics of the roulette wheel are employed as given parameters.

Variables, physical quantities, ideas, and results

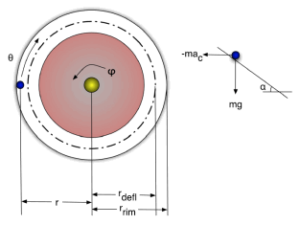In the figure (depicting a top view of the roulette wheel and the stator), the dotted line marks the circle of deflectors and the metrics of the wheel are represented by the radius of the rim circle (r rim), the radius of the deflectors circle (r defl), and the incline of the stator relative to the level plane (α).

Other metric variables for the dynamical system are: the position of the ball in polar coordinates (r is the distance of the ball to the centre of the wheel and θ the angle that the ball makes with the centre relative to a reference position – say, the 0 pocket), and φ as the angular position of the wheel relative to the same reference position. In the figure there are also drawn the forces acting on the ball in the incline plane of the stator (m is the mass of the ball, a c is the radial acceleration, and g is gravity).

By manipulating mathematically the equations of motion for the ball and wheel, we can express the time for which r, as a function of time r(t), equals r defl, that is, the time when the ball reach a deflector. Then, we can compute the instantaneous angular position of the ball and the wheel at the time it reaches a deflector, to obtain the angular location on the wheel directly below the point at which the ball strikes a deflector. The distribution of the resting place of the ball will depend only on this latter value. Such derivations are only possible under the assumption of a uniform distribution of the deflectors around the rim, which is met by most of the roulette wheels.

This model treats as essentially stochastic the trajectory of the ball after hitting the deflectors (which may be influenced by scatter induced by both the deflectors and possible collision with the frets).

For the case of a crooked table, the model is different, but relying on the same physical principles, and a new variable – the tilt angle – is introduced in the equations.

For a tilted roulette wheel, one can expect that the ball will favour leaving the rim on one half of the wheel. To a good approximation, the point at which the ball will leave the rim follows a uniform distribution over less that half of the circumference. In that case, the problem of predicting the final resting place is simplified to the problem of predicting the position of the wheel at the time the ball leaves the rim.

Experiments and implementation of the deterministic method

The deterministic model briefly presented (as any other in the same category) works in actual prediction only provided that the user has adequate measurements of the physical quantities that stand as initial conditions – velocities and accelerations – as well as roulette dimensions.

While roulette dimensions could be estimated directly or inferred from observational trajectory data, velocities and acceleration can only be measured with electronic devices. This of course renders the actual application very difficult, as the predictor “in action” must not raise any suspicion for the casino’s staff.

The input of the measured data and the computation leading to the output must as well be performed by a computing device, so it is optimal to have a device with integrated tasks of measuring and computing.

The tales about the successful attempts of prediction mention the computing device in various forms, but not enter the details of its construction and software. With the advent of the digital technology, in present days these tasks of measuring and computing can be fulfilled by an application on a smartphone.

By doing a search on the internet, you will find several such applications, claiming to be accurate in predicting the roulette outcome. Yet none of their developers give details about how their application works in regard to its measuring technology and the computing algorithms. Since the latter information actually reflect the kind of deterministic model used, in its absence we will never know what model the application uses. As such, to assess accuracy of the predictions we can only test them against the real outcomes, after buying the application.

But whatever advanced is the available technology, this does not make the deterministic model ultimately effective, since using a device in a casino was and will always be a hard and dangerous task.

Manual measurement for the initial conditions

The authors of the described model did not say in their paper whether they tested it in a real casino, and we may fairly assume they did not. Moreover, they did not use any device in their experimental lab-like tests. Instead, they propose a manual measurement supposed to replace the electronic measurement:

The approach was to record the time (in seconds) at which ball and wheel pass a fixed point. In their experiment they recorded from two spins of the wheel and 20 successive spins of the ball the timings T(i) and T(i + 1) of two successive revolutions, which actually are indirect measurements for the angular velocity observed over one complete rotation. From the relationship between the two Ts, one can determine the angular acceleration and deceleration.

The accuracy of such manual measurement is actually dependent on the physical hand-eye coordination of the observer. Of course, the manual measurement replaces only the measuring function of the prediction device, which still remains necessary for computation. Yet the software reverts to a simple computational one, easy to implement on a laptop or any personal digital assistant or a smartphone.

The two authors claim that their experiments indicate that is possible to accurately predict the correct half of the wheel in which the ball will come to rest. Concretely, they predicted the correct half of the wheel in 13 out of 22 trials, which gives an expected return over the long run of (36/18) × (13/22) – 1 = +18%.

Do the objective prediction methods have any future?

The Newtonian principle of action and reaction is reflected in people’s everyday life and not only in the physical interactions of bodies. Casino management always took countermeasures when the cheating attempts came to take systematic forms. This also includes any form of effective strategic play that uses uncommon abilities or skills. The famous Edward Thorp was banned in casinos because of its blackjack optimal strategy based on card counting and those applying methods of objective prediction in roulette has been threw out as well, as mentioned in the historical section of this article.

Casinos started to take care of their roulette tables once they noticed that physical imperfections favour the application of the statistical method of prediction. In present days it is hard to believe that imperfect tables are still in work, so we can fairly hypothesize that the statistical method has no future for the gamblers.

In what concerns the deterministic method, things moved faster. Although the “shoe-computer” or other devices hidden in the clothes of the gambler were treated like isolated exceptional cases of cheating, the phenomenon gave casinos a signal that such things are possible and improvable in time. With the advent of the smartphones and once applications for deterministic prediction came on the market, such methods of prediction came to be more and more applicable “in the field”. The straight and immediate reaction of the casinos was to introduce the random-speed rotor for roulette.

This device changes (randomly or by a certain algorithm) the speed of rotation of the stator between the spins and during the same spin as well, making the measurements of the initial conditions useless with respect to their input in the equations of the deterministic model.

Obviously, the ultimate move for the casino against the prediction attempts would be to use electronic roulette with outcome generated by RNG instead of the classical physical roulette. But unlike other casino games, the pleasure of playing roulette is strongly related to this traditional form, whose physical components and effects trigger sensations so specific to this game; so I suppose this won’t happen too soon.

In conclusion, if I were to give a straight answer to the question of whether predicting the outcome of roulette is possible, I would say that science says yes – it is theoretically possible; however, if you ask whether it is actually possible, the answer is time-dependent – what was possible yesterday could not be possible tomorrow.