Card Counting In Blackjack Versus Baccarat

Blackjack and baccarat resemble each other in many respects. Both are casino card games where players bet on a hand beating other hand as result of comparing the outcomes as totals of points.

Of course, rules are different, and the main difference between the two games is that in blackjack the player participates to making their hand and in baccarat the player bets on a dealer’s or on an imaginary player’s hand, participating to the game as a neutral bettor.

Form a game theory perspective, the two games have in common a strategic feature – both allow optimal strategies based on card counting.

In this article we compare card counting in blackjack and in baccarat, including in what concerns the effectiveness of this technique.

Using the optimal strategy

An optimal strategy, or basic strategy, in a game of chance is a mathematically-derived set of rules that the player must follow during the game for having an advantage over the house or their opponents relative to the non-strategic play.

This advantage should be understood in terms of comparison, not of actual gain in the game: Playing by an optimal strategy is mathematically proven to be better than not playing by one, but this does not guarantee a win in either short-, medium-, or long-run play.

The mathematical criteria by which an optimal strategy is constituted are: increasing the winning probability, maximising the profit and minimising the loss. Each game suitable for an optimal strategy has its own particularity with respect to these criteria, which can be employed all or in part in that strategy.

These criteria – when met – ensure the advantage of that strategy over other non-optimal strategies or the non-strategic play. In other words, optimal strategies reduce the house edge associated with the non-strategic play.

The last two criteria (regarding optimisation of profit and loss) are expressed by the following principle: the player should take that action which gives them the maximal expected value for their bet relative to the other possible actions.

In blackjack, optimal strategies use all three criteria, and tell the player when to raise, when to draw, when to stand, when to split, and when to double depending on the card configuration of that moment.

In baccarat, things are different. As in baccarat you bet on an outcome without being involved in its constitution (actually baccarat is a side bet itself), the only strategy available is to bet on the most probable outcome (Banker wins, Player wins, or a Tie) and the estimation of such probabilities is related to the card counting, as we will see further.

Card counting in blackjack

The extensive mathematical analysis of blackjack started in the 1950s. The first optimal strategy was based on the computation and comparison of the expected values of the possible actions (raising/not raising, hitting/standing, splitting/not splitting, and  doubling/not doubling) for all possible configurations of the board, that is, the dealer’s first card and player’s total.

Choosing the higher expected value in each of these situations gave what is called the fixed optimal strategy. It is called ‘fixed’ because it does not change with the particular values of the cards coming into play, but it takes into account just the hand total.

Things moved to the next level with the magnificent work of Edward Thorp (“the father of the card counting” as it is known in the gambling communities). The optimal strategy devised by Thorp was proved mathematically to give the player’s a higher (and significant) advantage over the house than the fixed optimal strategy. Thorp’s system was made public in his book Beat the dealer (1962), which sold over 500,000 copies, but it also has been tested successfully in casinos by gamblers and by the author himself, who ended by being banned by the casinos across the US.

Thorp’s idea was to assign weights to each card value and use a counting system based on these weights in order to adjust the probabilities for the various totals of points as the cards are dealt. The counting system provides approximations of the probabilities of the card values in the rest of the deck conditional on the result of the count.

Such an approach yields a more accurate comparison of the expected values in each possible situation and action and as such improves and fine-tunes the fixed optimal strategy. The card-counting strategy exposes more situations in which the expected value is positive than the fixed optimal strategy.

Thorp’s counting system is called the high-low system and the weights are as follows:

• +1 for values 2 through 6;
• –1 for 10, face cards, and ace;
• 0 for the remainder.

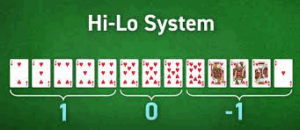With the first card dealt, one may begin the count (called the ‘running count’). The running count is converted to what is called the true count (the running count divided at the number of decks used). Depending on the true count, dealer’s first card and player’s total (and player’s cards, for the splitting action), the high-low optimal strategy tells the player what is their optimal move at every moment of the game.

This strategy is expressed for an easier learning as ready-to-use strategic charts that you may find in the most of the blackjack strategy resources on the internet. However, its application is not easy, as it requires skills, including the card counting one.

Since the 1960s, several counting systems for blackjack have been developed (Omega II, Hi-Opt I, Hi-Opt II, Wong halves, Red 7, KO, and Zen, to name the most popular).

Such counting systems rely on the same basic math that an optimal blackjack strategy is derived from; they are just different methods of approximations for updating the probabilities involved and there are no mathematical criteria by which they can be ranked with respect to accuracy or effectiveness. It’s just that some are easier to be applied in practice than others.

As for effectiveness, a card-counting optimal strategy (applied properly) will reduce the blackjack house edge significantly: Known in the range of 0.5% – 2.7% for the non-strategic play, depending on the blackjack version, a card-counting strategy can reduce the house edge down to 0.1% (which is not a figure to be seen in other casino games).

Card counting in baccarat

One may fairly ask the question: Since in baccarat the player does not participate to making any hand (as in blackjack), but just places bets on the outcomes, can the baccarat winning odds or expected return be enhanced?

The answer is yes, both the odds and expected value of the bets can be enhanced, but only in certain circumstances and through a card counting strategy.

Since in baccarat you may bet on either the Banker, Tie, or the Player as a neutral observer, enhancing your odds or return reverts to placing your bet only when you have information that changes the odds in the favour of a side or another. Such information is only available when multiple hands are played before the shoe is shuffled; it is a situation when you can keep the track of the cards dealt before placing your bet. With every card dealt, the odds of one side or another winning (or a tie) change. Therefore, keeping track of the cards and using a counting algorithm, you may find when the odds incline in a side or another.

How will such a count contribute to an optimal strategy? That’s simple – for certain running counts, you should bet on the Banker, on the Player, even on a Tie, and for certain counts you should not place any bet. Applying such a strategy in practice is far simpler than in baccarat, as the number of the possible actions and card configurations are far lower.

As in blackjack, several counting systems were devised for baccarat. One popular system is the following:

• +1 for ace, 2, 3
• +2 for 4
• –1 for 5, 7, 8
• –2 for 6
• 0 for 9, 10, J, Q, K.

Edward Thorp came with his own counting system in baccarat, a bit more complicated than the one above.

The systems are built on the idea that as the count increases the Player bet’s odds increase, and as the count decreases, the Banker bet’s odd increase. These counting systems only aim at placing a Banker or a Player bet, as their probabilistic approximations can tell nothing about the tie, which anyway is very rare.

Yet a baccarat analyst (John May) devised a counting system exclusively for the Tie bet. May showed that if there are no odd cards remaining in the shoe, then there are only five possible hand totals, namely 0, 2, 4, 6, and 8; in these circumstances, the odds of a tie are doubled, and given the high payout odds of this bet, it worth placing it. His counting system is very simple: Start the count from zero and add 1 for every odd card that is dealt. When the count reaches 160, it is time to place a Tie bet.

As in blackjack, the true count will say when a certain betting action is recommended. Unlike blackjack, where the card counting strategy will tell you what the optimal play is during the entire game, in baccarat it tells you when to play and when not. The running count determines breakeven points (where house edge is zero), beyond which the expectation is positive. However, for this advantage over the house to be materialised, it is important to play only in those positive situations in the long run, hold your bet in the rest of them, and wait for the next favourable one.

While the math behind such strategies is incontestable, the question arises as how effective a card-counting strategy actually is in baccarat.

The effect of the card-counting strategy in baccarat

No. of decks	Banker	Player	Tie
8	0.010579	0.012351	0.143596
6	0.010558	0.012374	0.144382
1	0.010117	0.012864	0.157461

Baccarat is the casino game offering the second-lowest house edge for its bets (blackjack is in the top with its optimal play). The table above notes the house edge of the Banker, Player, and Tie bets depending on the number of decks used in the game.

With such small differences in the values of the house edge for the various numbers of decks, it is obvious that casinos do not choose to play the game with more decks for their house edge gain, but rather for making card counting more difficult for the bettors.

Now let’s see what the effect of one card being removed from the shoe is on the house edge. This effect is given in the next table, where minus means a decrease and plus an increase in house edge:

Effect of card removal on house edge (8 decks)

Card Removed	Banker	Player	Tie
0	0.000019	-0.000018	0.000513
1	0.000044	-0.000045	0.000129
2	0.000052	-0.000054	-0.000239
3	0.000065	-0.000067	-0.000214
4	0.000116	-0.000120	-0.000292
5	-0.000083	0.000084	-0.000264
6	-0.000113	0.000113	-0.001160
7	-0.000083	0.000082	-0.001091
8	-0.00005	0.000053	0.000654
9	-0.000023	0.000025	0.000426

In the table entries, a value with minus reflects an advantage for the bet on Player and a positive value reflects an advantage for the bet on Banker. Of course, any new card dealt may change this advantage.

Even from this table one can see how minute the effect is. Indeed, the effect increases with the number of cards removed, but even if you multiply the values by 100 (a non-realistic number of cards dealt at a table), the effect still remains minute.

This observation is confirmed by the results of the following statistical analysis made by mathematician Michael Shackleford.

The true count can indicate situations in which the house edge passes the breakeven point. The next table shows the ratio of hands played, based on a simulation of 100 million hands, for which the true count passes the zero house edge point. Penetration indicates the ratio of cards dealt before the cards are shuffled.

Positive Expectation

Penetration	Banker	Player	Tie
90 percent	0.000131	0.000024	0.000002
95 percent	0.001062	0.000381	0.000092
98 percent	0.005876	0.003700	0.002106

In terms of profit, apply the values of the above table for 100 bets and $1,000 stake every time a positive expected value occurred and you get:

Expected profit for the optimal play based on positive expectation

Penetration	Banker	Player	Tie
90 percent	$0.01	$0.00	$0.00
95 percent	$0.20	$0.06	$0.15
98 percent	$2.94	$1.77	$11.93

We can see how low the profit rate is. The strategic play based on card counting reduces the house edge, but not that much. For example, with an optimal strategy, the house edge of the bet on the Banker comes to 0.99% compared to the house edge of 1.06% for that bet when not counting cards.

Besides the numbers, optimal play based on card counting assumes that both the player and the casino is not going to mind if the player will only make a bet once every tens or hundreds of hands.

Conclusion

Card counting is a technique serving an optimal strategy in blackjack and baccarat. In blackjack the card-counting optimal strategy is applicable in any situation and circumstances, indicating the player the optimal action in terms of expectation.

In baccarat card counting is only applicable in particular circumstances, namely when multiple hands are played before the shoe is shuffled, giving the bettor the opportunity to track the cards dealt before they place their bet. Card-counting optimal strategy in baccarat indicates the player when to bet and on what side, but only when the count is favorable for such bets and thus several bets should be hold until such a situation occurs.

While in blackjack the gain in house edge is significant when using a card-counting optimal strategy, in baccarat such a gain is far lower than in blackjack.

Optimal strategy is based on optimising expected value and as such it can only be materialised over the long run; this is true for both games. However, in baccarat, playing only when it is advantageous assumes skipping bets in the order of hundreds. The very low gain in house edge along with this practical inconvenient makes the card-count strategy in baccarat not worth the bother.